clustreing-ensembled-demo

Clustering Ensemble

这篇主要是记录如何进行集成选择，4种不同的方法

1. 基于特征的方法（n×L矩阵，如图（a）所示）
   
2. 基于聚类的方法（n×NC矩阵，如图（b）所示
   
3. 基于样本协关联的方法（n×n矩阵，如图（c）所示）
   
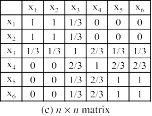
4. 基于聚类相交的方法（NC×NC矩阵，如图（d）所示）
   

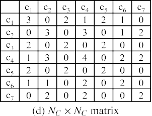
   import numpy as np
   import pandas as pd
   from matplotlib import pyplot as plt
   from pandas import DataFrame
   from sklearn.cluster import KMeans
   from sklearn.cluster import AgglomerativeClustering
   from scipy.cluster.hierarchy import dendrogram, linkage
   x1 = [100,100]
   x2 = [95,95]
   x3 = [70,70]
   x4 = [50,53]
   x5 = [30,30]
   x6 = [20,20]
   #   将其放入矩阵中然后填充到数据框里
   stuMatrix = [x1,x2,x3,x4,x5,x6]
   df = DataFrame(stuMatrix, columns=['att1', 'att2'])
   
   # 用k-means聚类 聚成k类
   def kmeans1(data,k):
       iteration = 50
       data_zs = 1.0*(data - data.mean())/data.std()  # 数据标准化
       model = KMeans(n_clusters=k, max_iter=iteration)  # 分为k类，并发数4
       model.fit(data_zs)  # 开始聚类
       #   详细输出原始数据及其类别
       r = pd.concat([data, pd.Series(model.labels_, index=data.index)], axis=1)
       return (r)
   
   C1 = kmeans1(df,2)
   C3 = kmeans1(df,3)
   # 层次聚类
   def agglomerative(data,group_size):
       cls = AgglomerativeClustering(n_clusters = group_size,linkage = 'ward')
       cluster_group = cls.fit(data)
       #   详细输出原始数据及其类别
       r = pd.concat([data, pd.Series(cluster_group.labels_, index=data.index)], axis=1)
       return (r)
   
   C2 = agglomerative(df,2)
   
   a1 = C1[C1.columns[-1]]  #取C1数据框的最后一列
   a2 = C2[C2.columns[-1]]
   a3 = C3[C3.columns[-1]]
   #   取出数据在不同聚类结果中的类别情况，输出论文中的a矩阵
   a_Matrix = pd.concat([a1,a2,a3],axis=1)
   a_Matrix = np.array(a_Matrix)
   print(a_Matrix)
   
   # #   直接创建b矩阵
   # data = {"c1":[1,1,1,0,0,0],"c2":[0,0,0,1,1,1],"c3":[1,1,0,0,0,0],"c4":[0,0,1,1,1,1],"c5":[1,1,0,0,0,0],"c6":[0,0,1,1,0,0],"c7":[0,0,0,0,1,1]}
   # b_Matrix = pd.DataFrame(data,index=[0,1,2,3,4,5])
   # b_Matrix = np.array(b_Matrix)
   # print(b_Matrix)
   
   # 构造协关联矩阵
   co_matrix = np.ones((6,6))  # 6为样本个数
   
   for m in range(5):  # m为第m个样本
       for n in range(m+1, 6):  # n为第n个样本
           sum_support = 0
           for l in range(3):  # 3为参数，代表算法个数
               if a_Matrix[m, l] == a_Matrix[n, l]:  # 如果第l个算法认为第m个样本和第n个样本是同一类
                   sum_support += 1  # 支持在一起的票数+1
               else:  # 如果第l个算法都没有选中fm,fn
                   sum_support += 0  # 支持在一起的票数+0
           co_matrix[m,n] = sum_support/3  # 计算第m个样本和第n个样本之间的稳定性 = 支持在一起的票数（即支持在一起算法数）/总算法数
           # 以上得到的co_matrix仅是上三角矩阵，将其进行对称矩阵变换
           co_matrix[n, m] = co_matrix[m, n]
   
   print(co_matrix)
   
   # 构造b矩阵
   # get_dummies 是利用pandas实现one hot encode的方式
   b = pd.DataFrame()
   for i in range(a_Matrix.shape[0]):
       int_as_str = [str(number) for number in a_Matrix[i, :]]
       int_as_str = pd.DataFrame(int_as_str).T
       b = pd.concat((b,int_as_str),axis=0)
   print(b)
   # b.columns = ['first',  'second', 'third']
   b_Matrix = pd.get_dummies(b)
   print(b_Matrix)
   
   # 比较两个数组相同位置相同值有几个
   def campare(arr1,arr2,val):
       sum = 0
       for i in range(len(arr1)):
           if arr1[i] == arr2[i] and arr1[i] == val:
               sum +=1
       return sum
   
   # 构造d矩阵
   d = np.array(b_Matrix)
   print(d)
   aaa = []
   for i in range(d.shape[1]):
       c1 = d[:, i]
       for l in range(d.shape[1]):
           c2 = d[:, l]
           # num为b矩阵中第i列与第j列相同1的个数，反应的是不同算法在聚类时重合的样本数量
           num = campare(c1, c2, 1)
           aaa.append(num)
   aaa = np.array(aaa)
   d_matrix = aaa.reshape(d.shape[1],d.shape[1])
   print(d_matrix)